Grundrechenarten schriftlich
Beim schriftlichen Rechnen immer gut lesbare Ziffern schreiben
und diese immer sauber neben- und untereinander positionieren.
Am besten verwendet man Rechenpapier mit Kästchen.
Addition schriftlich
Bei der schriftlichen Addition schreibt man die zu addierenden Zahlen rechtsbündig untereinander.
Hat man nur 2 Zahlen zu addieren, so notiert man die größere oben.
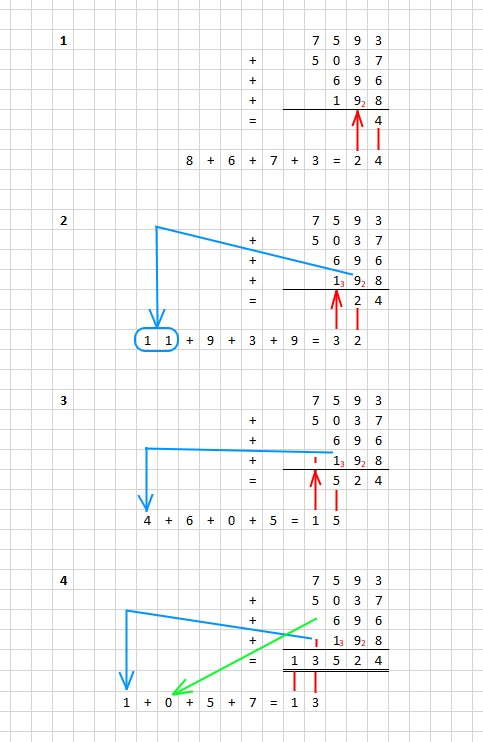
Die Anzahl der Additionsschritte ist gleich der Ziffernanzahl der größten Zahl.
Addition von 2 Zahlen
Die Addition erfolgt immer von rechts nach links und von unten nach oben:

Die größere Zahl ist 5-stellig, also hat die Addition 5 Schritte.
Addition mehrerer Zahlen
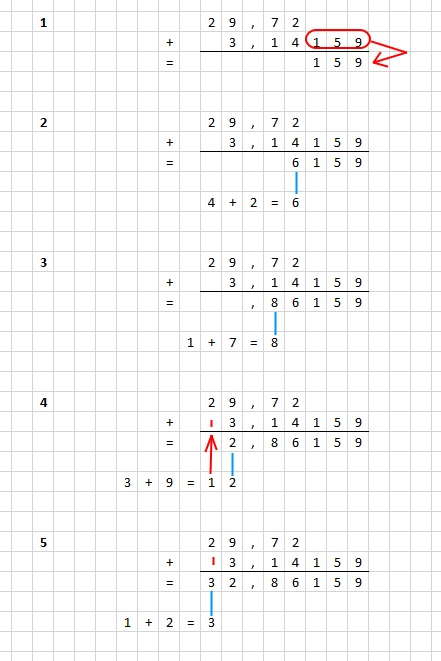
Addition mit Komma
Bei der Addition müssen die Zahlen so untereinander geschrieben werden, dass alle Kommas genau untereinander stehen.
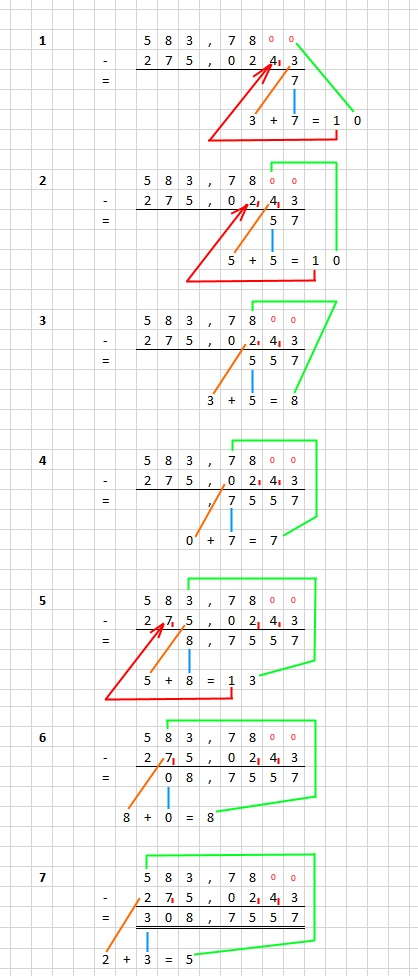
Subtraktion schriftlich
Bei der schriftlichen Subtraktion schreibt man die beiden Zahlen rechtsbündig untereinander.
Der Minuend, also die Zahl, von der etwas abgezogen werden soll, kommt nach oben.
Der Subtrahend, also die Zahl, die abgezogen werden soll, kommt nach unten.
Ausnahme:
Ist der Subtrahend größer als der Minuend, kommt die größere Zahl nach oben
und man setzt von vornherein ein Minuszeichen vor die Ergebniszeile.
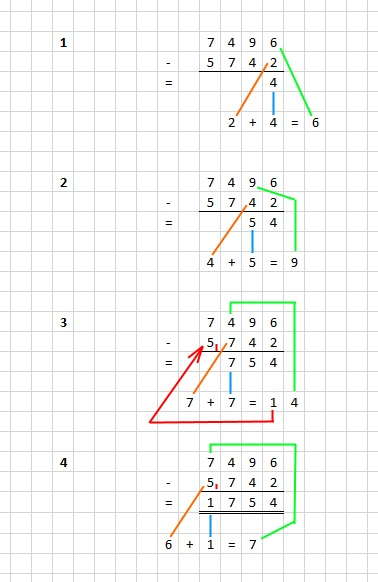
Auch bei der schriftlichen Subtraktion ist die Anzahl der Rechenschritte gleich der Ziffernzahl der größten Zahl.
Man rechnet wieder von rechts nach links und von unten nach oben:
Einfache Subtraktion
Normale Subtraktion
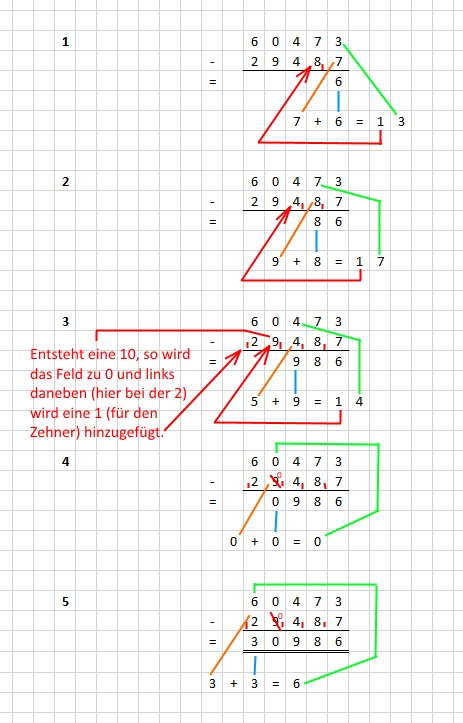
Subtraktion mehrerer Zahlen
Soll man mehrere Zahlen von einer Zahl a subtrahieren, so addiert man zunächst
alle Subtrahenden und subtrahiert dann deren Summe von a gem. folgendem Schema:
\documentclass[8pt]{article}
\begin{document}
$$ a - b - c - d = a - (b + c + d) $$
\end{document}
Subtraktion mit Komma
Wie bei der Addition müssen die Zahlen so untereinander geschrieben werden, dass alle Kommas genau untereinander stehen.
Multiplikation schriftlich
Voraussetzung für die schriftliche Multiplikation ist das solide Kopfrechnen mit dem kleinen Einmaleins.
Bei der schriftlichen Multiplikation schreibt man die beiden Zahlen hintereinander, getrennt durch einen Punkt oder ein x.
Üblicherweise schreibt man die längere Zahl zuerst.
Normale Multiplikation

Multiplikation mit einer Kommazahl
Aufgabe: Wir benötigen möglichst genau das Vierfache der Kreiszahl pi.
\documentclass[8pt]{article}
\begin{document}
$$ \pi = 3,14159265 $$
\end{document}
Wir schreiben:

Das Ergebnis muss immer soviele Nachkommastellen haben wie Multiplikand und Multiplikator zusammen.
In diesem Fall hat pi 8 Nachkommastellen, die 4 keine.
Die Summe ist also 8. Somit muss das Ergebnis 8 Nachkommastellen haben.
Multiplikation mit zwei Kommazahlen

Der Multiplikand hat 3, der Multiplikator 2 Nachkommastellen. Die Summe ist 5.
Also muss das Ergebnis 5 Nachkommastellen haben.
Ganz zum Schluss setzt man das entscheidende Komma (im Bild rot).
Division schriftlich
Voraussetzung ist auch hier das solide Kopfrechnen mit dem kleinen Einmaleins.
Bei der schriftlichen Division schreibt man die beiden Zahlen hintereinander, getrennt durch einen Doppelpunkt.
Die zu teilende Zahl (Dividend) kommt zuerst, danach der Teiler (Divisor).
Einfache Division ohne Rest
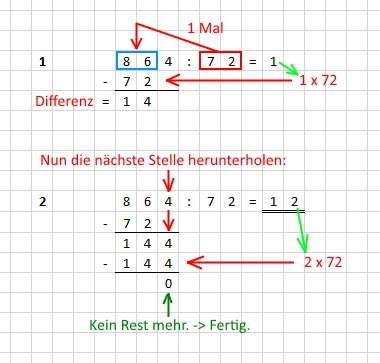
Erläuterungen:
Schritt 1:
Man greift vom Dividend (linke Zahl) von links soviele Stellen ab (blau), dass
eine Zahl entsteht, die gleich groß oder möglichst wenig größer als der Divisor ist.
Im Beispel passt die 72 einmal in die 86 ud es bleibt ein wenig Rest.
Das Produkt 1 x 72 = 72 schreiben wir unter die 86 und bilden die Differenz: 14.
Schritt 2:
Wir holen nun die nächste Stelle (im Beispiel die 4) aus dem Dividend hinter den Rest herunter.
Es entsteht die Zahl 144.
Nun probieren wir aus, wie oft die 72 in die 144 passt: genau 2 Mal.
Das Produkt 2 x 72 = 144 schreiben wir unter die 144 und bilden die Differenz: 0.
Ist die letzte Ziffer des Dividenden (im Beispiel die 4) bearbeitet und der Rest = 0, sind wir fertig.
Division mit einer Kommazahl
Wir bestimmen den Quotienten 1410,312 : 24
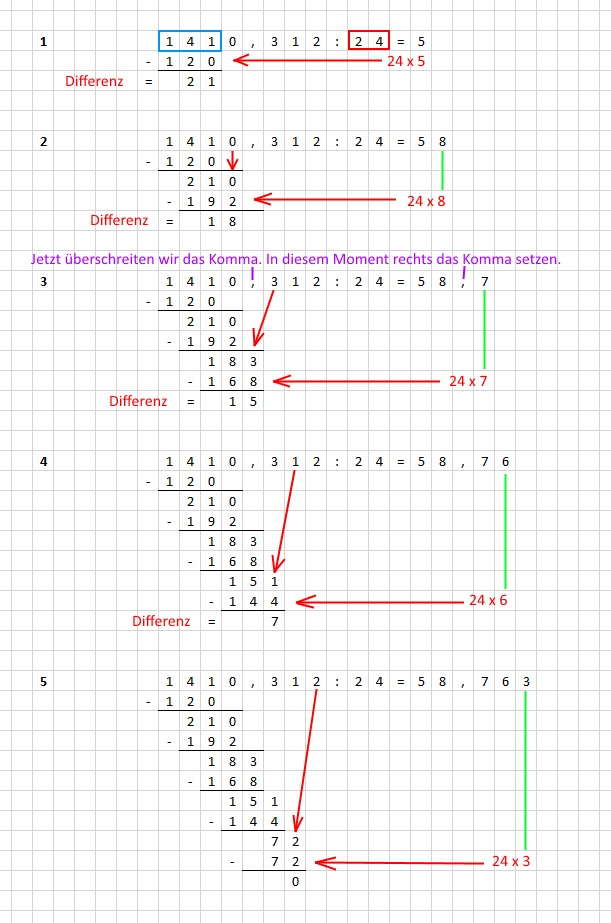
Ist die letzte Ziffer des Dividenden (im Beispiel die 2) bearbeitet und der Rest = 0, sind wir fertig.
Division mit zwei Kommazahlen
Das geht zwar auch, ist aber hoch fehleranfällig, da es zwischendurch immer wieder Additionen von Kommazahlen erforderlich macht.
Das einfache Zahlenschieben (Kästchen unter Kästchen) ist dann nicht mehr möglich
Daher verwendet die Schulausbildung hierfür einen anderen Weg:
Das Komma wird bei beiden Zahlen um soviele Stellen nach rechts geschoben, bis es bei der rechten Zahl ganz weg ist.

Nach der Kommaverschiebung dividiert man nach Schema F wie oben bereits gezeigt.
Das Ergebnis der Division bleibt dabei das gleiche. Warum?
Mathematisch ist das Verschieben des Kommas bei beiden Zahlen um die gleiche Stellenzahl eine Erweiterung des Bruches um den Faktor 10n,
wobei n die Anzahl der Stellen ist, um die das Komma verschoben wurde.
Schauen wir uns das einmal mit Bruch-Strichen an:
\documentclass[8pt]{article}
\begin{document}
$$ x = \frac{36593,74}{6,289} = \frac{36593,74 \cdot 10^3}{6,289 \cdot 10^3} = \frac{36593,74 \cdot 1000}{6,289 \cdot 1000} = \frac{36593740}{6289} $$
\end{document}
Der Bruch ganz rechts gibt exakt die Aufgabe wieder, wie sie auf dem Rechenblatt mit der Kommaverschiebung erreicht wurde.











